問題
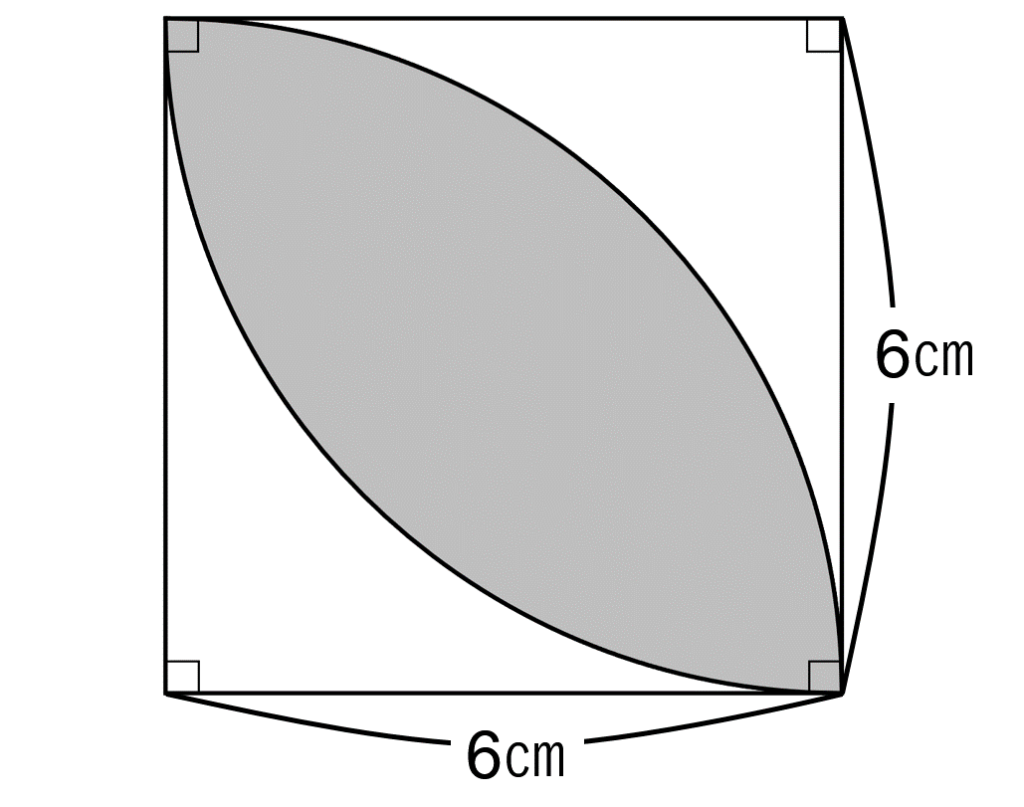
図形の影になっている部分の面積を求めて下さい。尚、円周率は下を用いて下さい。
中学生以上:円周率=π
小学生:円周率=3.14

これはとても有名な問題なので、皆さんどこかで見たことがあるかもしれません。しかし、この問題からは、「答えを求める!」ということ以上に多くのことを吸収できます。
なんだと思いますか??
とりあえず、今から解法を2つ紹介したいと思います。
解法1:困難は分割せよ!
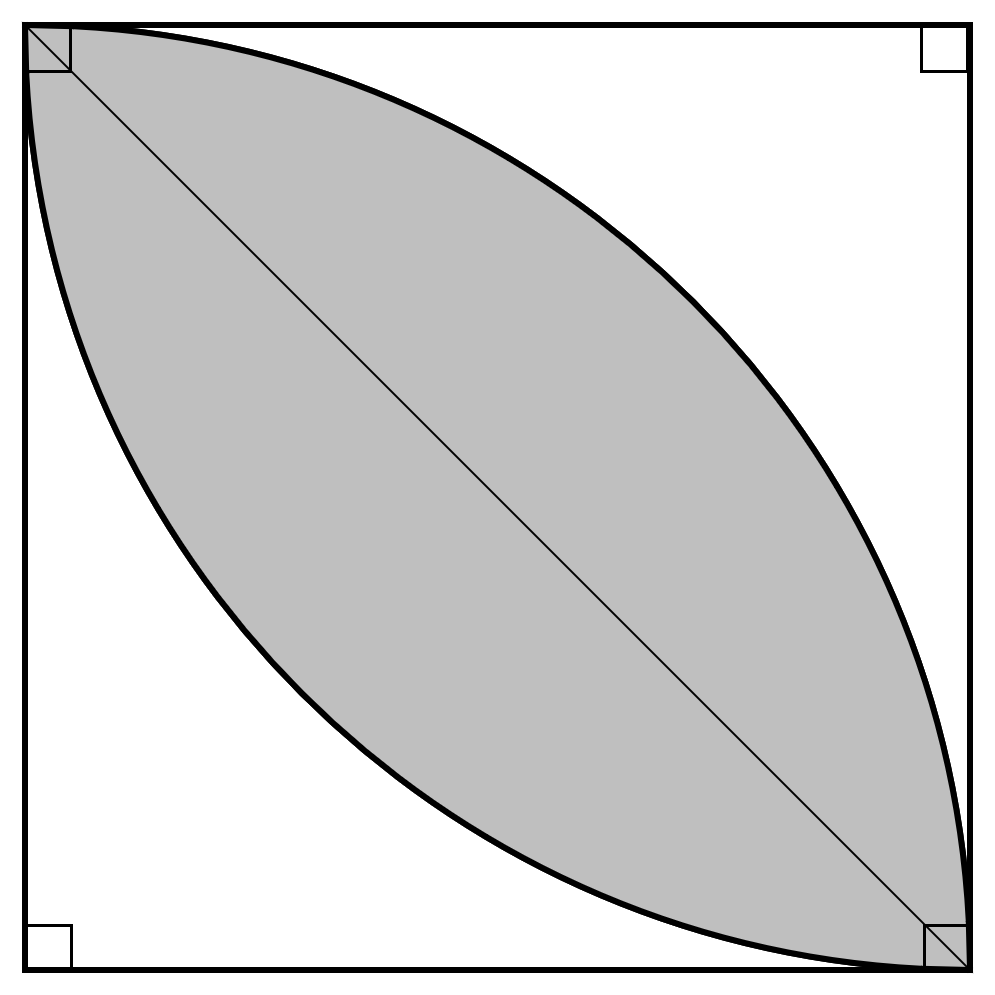
求められている面積は、「種」のような形をしていて、当然私たちが知っている面積公式を使って一発で求めることは出来ません。
数学者であるデカルトの言葉に「困難は分割せよ」というものがあります。
デカルトについては、またの機会にゆっくりとお話しします。(かなり長くなる危険があるので・・・)
話は戻りますが、複雑な図形は補助線などでその領域を分割し、知っている図形を組み合わせることを考えましょう!
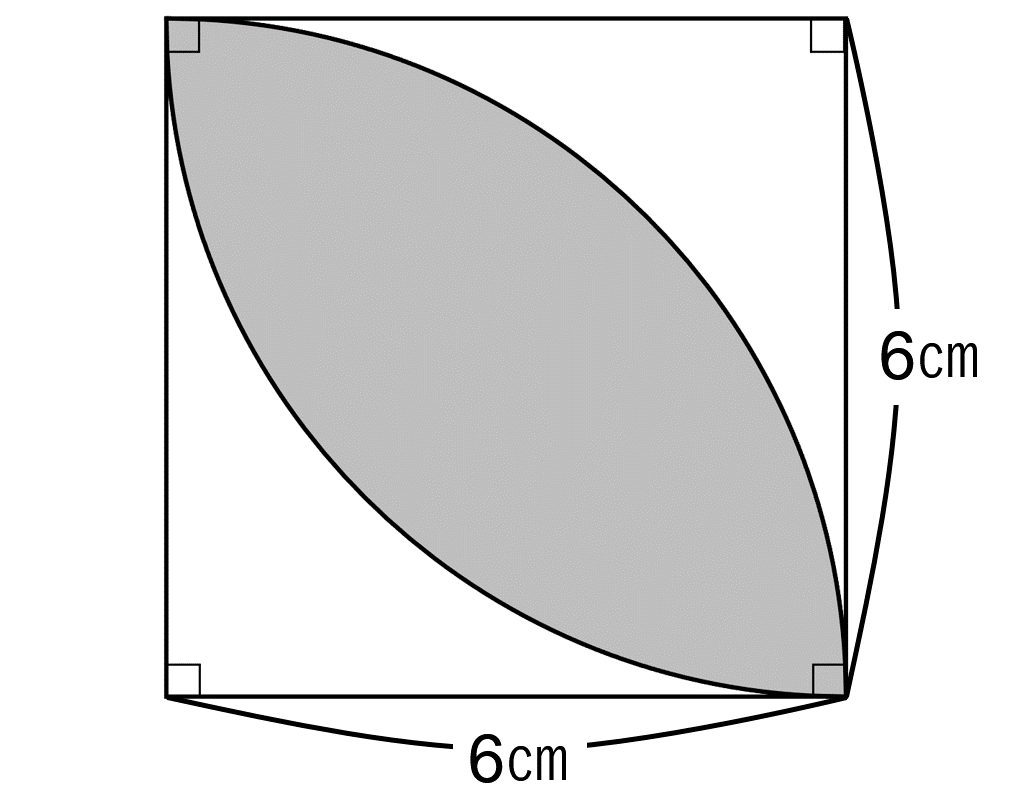
上図のように、対角線を引くことで「種」の半分の面積を求めることが出来ます。
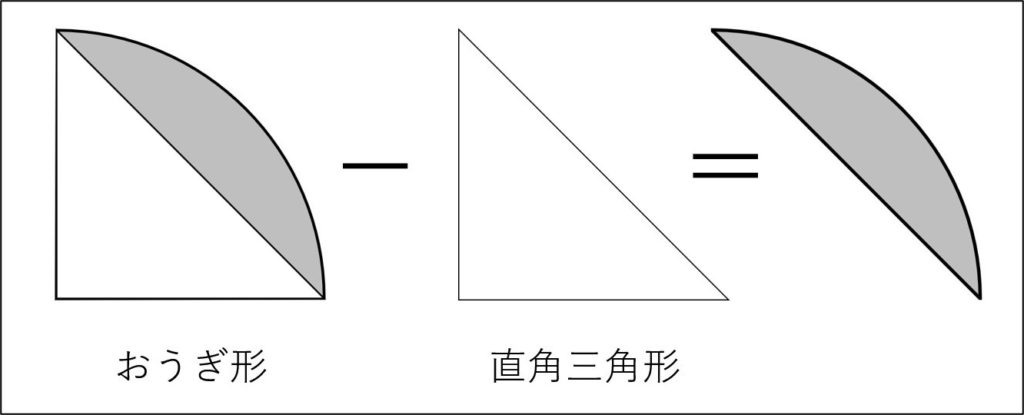
(おうぎ形の面積)=6×6×π÷4=36π÷4=9π
(直角三角形の面積)=6×6÷2=18
よって、(「種」の半分の面積)=(おうぎ形の面積)ー(直角三角形の面積) となります。
つまり 9πー18 となる。
求める面積は2つ分なので (9πー18)×2=18πー36 ㎠
※小学生は 18×3.14ー36=20.52 ㎠
「困難は分割せよ!」
複雑な図形は補助線などを用いて分割し、知っている図形から求めることが出来ないかを考える。
解法2:ダブりを意識せよ!
「解法2」は「解法1」とアプローチが異なり、「種」の重なりを考えます。下の図を見てみましょう。
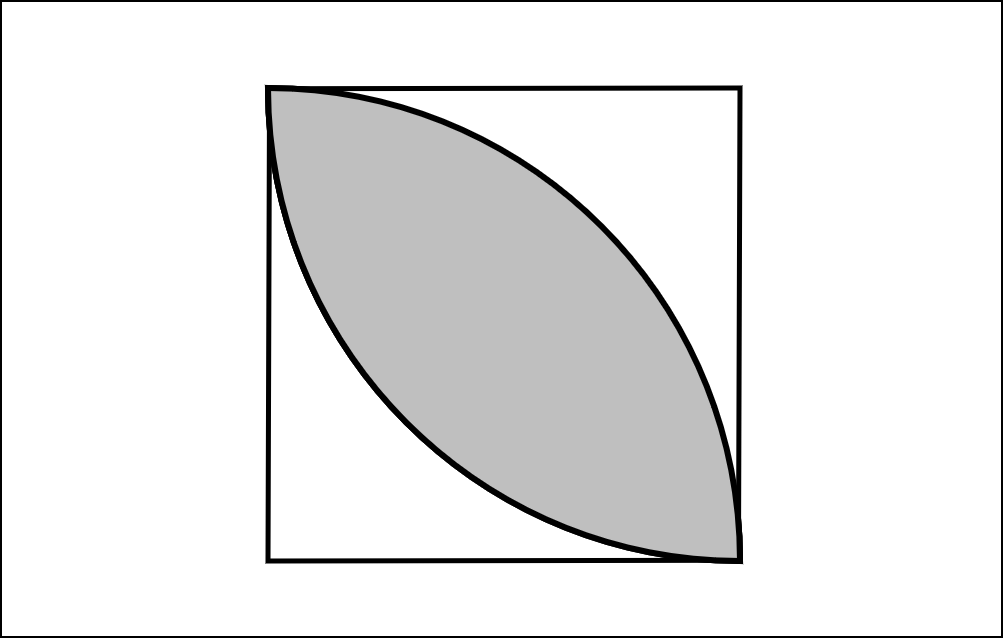
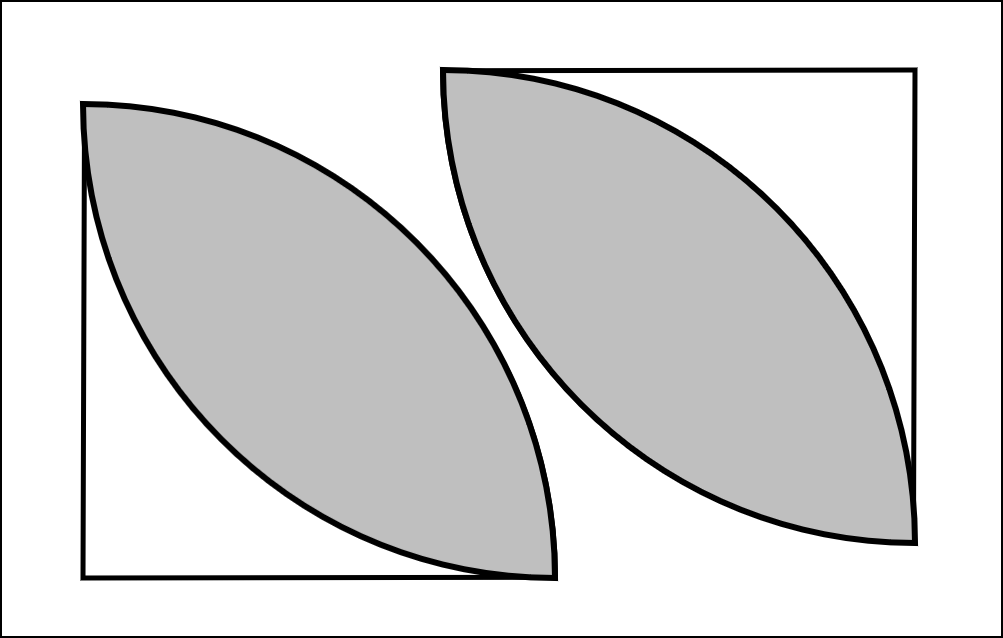
正方形が2つの「おうぎ形」に分かれます。
言い換えると、おうぎ形の面積2つ分では、「種」の面積が1つ余計に求まってしまうのです。(集合で「べん図」を学習している人は、イメージしやすいと思います。)
つまり、求める面積は、(おうぎ形の面積)×2-(正方形の面積)となります。
(おうぎ形の面積)=6×6×π÷4=36π÷4=9π
(正方形の面積)=6×6=36
よって、9π×2-36=18π-36 ㎠
※小学生は 18×3.14ー36=20.52 ㎠
求める面積を2つの図形の重なり部分ととらえ、余計な1つ分の面積を取り除く。
まとめ
いかかでしたでしょうか??
ほとんどの方が「解法2」の方がラクだと感じたでしょう。しかし、ここに数学の落とし穴があります。「解法2]は今回の問題のような特別なタイプの問題にしか用いることが出来ません。
一方で、「解法1」は答えを求めるために手間はかかりましたが、あらゆる問題に用いることが出来る考え方です。
数学や算数では、いわゆる頻出問題を学習することによって、目の前にある問題だけが解ければ良いのではなく、アプローチの仕方を学ぶことが求められます。そういった意味では、この問題では「解法1」も「解法2」もしっかりと理解する必要があります。
テストなどで、見たことがある問題が出題されれば、早く解ける解法が理想的であることは言うまでもありません。しかし、レベルの高いテストであればあるほど、見たことの無い問題に出くわす可能性は高くなります。
この問題に限らず、別解を学ぶことには、このような重要な意味があるのです。
今回の「円を含む面積」の問題は以下のプリントで演習が行えます。是非チャレンジしてみましょう!
ここまで読んで下さりありがとうございます。また次回のブログでお会いしましょう!!


コメント